by Susmita Adhikari
Dark matter halo formation
There are many open questions that remain about the matter that surrounds us and makes all of us up. Two major ones that astrophysicists currently ponder are: the nature of a large fraction of the matter itself; and where the general theory of relativity, Einstein's description of how gravity works, breaks down and must be extended by a more expansive theory that can play well with quantum physics, since right now it doesn't do that.
Cosmologists are always looking for good ways to probe these questions and try to elucidate them, and a fairly recent one that they have found quite compelling is to figure out a way to define the edges of the largest conglomerations of matter in the Universe. It would be most excellent if these structures could lend us some insight into these matters, so to speak.
To step back for a moment to things we do know: a small percentage of the total matter content of the Universe is made of normal visible matter made of protons, neutrons and electrons (almost entirely) and generally termed "baryonic matter" by cosmologists. The rest is largely a mysterious component that thus far only interacts gravitationally with the rest of the Universe, and which we call dark matter. As best we can tell, there is six times more dark matter in the Universe, by mass, than baryonic matter. A large fraction of this dark matter exists in the form of "halos," concentrated clumps held together by their mutual gravitational interactions.
Halos are the result of a long sequence of cosmic structure formation. Cosmic archaeology tells us that halos formed something like this: The early Universe, after a very short period of rapid expansion called inflation, settled into its current phase of more leisurely general cosmic expansion (or "Hubble flow," as cosmologists often call it). At the end of inflation, while the density of matter—on average—had been smoothed out to become very homogenous on large scales, small quantum perturbations were amplified to more significant density fluctuations—places where there was a tiny bit more, or less, matter. The knots of slightly higher density served as wells of gravitational potential and began to grow further with time by attracting ever more matter through gravity.
Once matter fell into one of these potential wells it detached from the overall expansion of the Universe and began to orbit within the wells themselves. In other words, the velocity of matter particles in a given well became determined much more by the gravity within the well than by the cosmic expansion.
Fast forward to today. Depending on its location in the potential well, a given particle may have quite a different velocity than a test particle at the same distance from us moving with the Hubble flow. These dense (relative to the rest of the much emptier Universe), swirling conglomerations of dark and baryonic matter are what make up halos.
To distinguish between the two primary components of halos, let us look at the consequences of the fact that baryonic matter particles can emit light through interactions with other particles and collide with one other, causing them to radiate away energy and lose angular momentum, respectively—further causing them to sink to the centers of halos where they form the galaxies, stars and all the multitude of elegant and beautiful things that are visible to us.
On the other hand, dark matter interacts only gravitationally (with itself, and all other matter) as far as we have thus seen, and can, at very best, interact with normal matter only slightly through forces other than gravity. And, since the “stickiness” of normal matter that arises from electromagnetic effects is what predominantly causes it to clump together in a significant way, dark matter, which doesn't interact electromagnetically, remains puffed out in the halo. This causes it to extend large distances outward from the galaxy that forms at its center.
What we want to do is use the halos to learn about the particles that compose them. And what we see in simulations is that the inner structure and growth over time of dark matter halos is not only related to the individual initial density perturbations in the early Universe that collapsed to form them but also to the environment in which they grew. A region in the Universe where particles are in orbit around a central potential eventually forms a stable energetic configuration when the net potential energy and the kinetic energy of the system is in equilibrium. Such a structure is said to be virialized, which means the system as a whole satisfies the “virial condition,” where the kinetic and gravitational potential energies of the constituent particles balance each other out. A good understanding of this process can give us insight into some of the fundamental questions in cosmology, such as how and why galaxies look the way they do.
To the halo's edge
Traditionally the boundary of a halo is defined as the radius from the center of the halo within which the density of matter is about 200 times the average density of the Universe. This definition is derived from what’s called the simplified spherical collapse model, which follows the collapse of a shell enclosing a spherical sharp-edged region of higher density in an expanding Universe. From the center of the halo, the shell initially appears to expand with the Hubble flow like everything else, but when enough mass has accreted within it the shell starts to collapse (called “turn-around”) due to the gravitational force of the excess mass within it. In this picture the mass inside the shell is assumed to be constant in time. However, it’s possible for accreting matter to form multiple shells within a sphere, and the assumption of constant mass is true only as long as different shells of matter within the sphere do not cross each other.
Once particles begin to orbit at varying rates inside of the sphere, the shells that make them up can actually cross each other as the halo evolves, which we refer to as, unsurprisingly, “shell crossing.” At this point, the mass inside is no longer constant. The spherical collapse model overcomes this problem by halting the evolution of each shell half-way from turn-around, since at that point the energetics of the system as a whole satisfy the virial condition and the overdensity enclosed within is nearly 178 times the background in a matter-dominated Universe. This is called the virial radius of the halo. This conventional definition, however, often does not form the true boundary of a halo and is an approximation—many halo effects are known to persist outside of this boundary.
Why the definition of a halo's “edge” matters
My work has been related to understanding the boundaries of dark matter halos. While the dark matter inner structure has been studied extensively, the boundaries of a halo can also contain interesting cosmological information. In principle there exists a physical boundary to a halo if one describes a halo as a region within which multiple streams of particles are on orbits. We define this boundary as the distance at which the most recently accreted matter reaches the farthest point in its orbit after it falls into its cluster (technically called the apogee after first infall).
In the idealized spherical picture, this distance forms a shell itself, and divides space into two distinct regions. The inner region has objects that have dark matter shells and streams that are in orbits that constantly cross each other, and the exterior region has still-infalling matter that has never completed a single orbit within the halo potential. At the location of the shell, the radial velocity of particles relative to the center of the halo approaches zero. As a result, particles spend a longer time at this radius and thus “pile up” to form what is referred to as a “density caustic,” a sudden rise in particle density in a narrow localized region. In idealized simulations this caustic is clearly visible as spike in the density profile, as can be seen in Figure 2, and essentially marks the boundary of a halo (“caustic” in this sense is an adaptation of a mathematical term meaning a very sharp boundary in space where density spikes; see, for example, here).
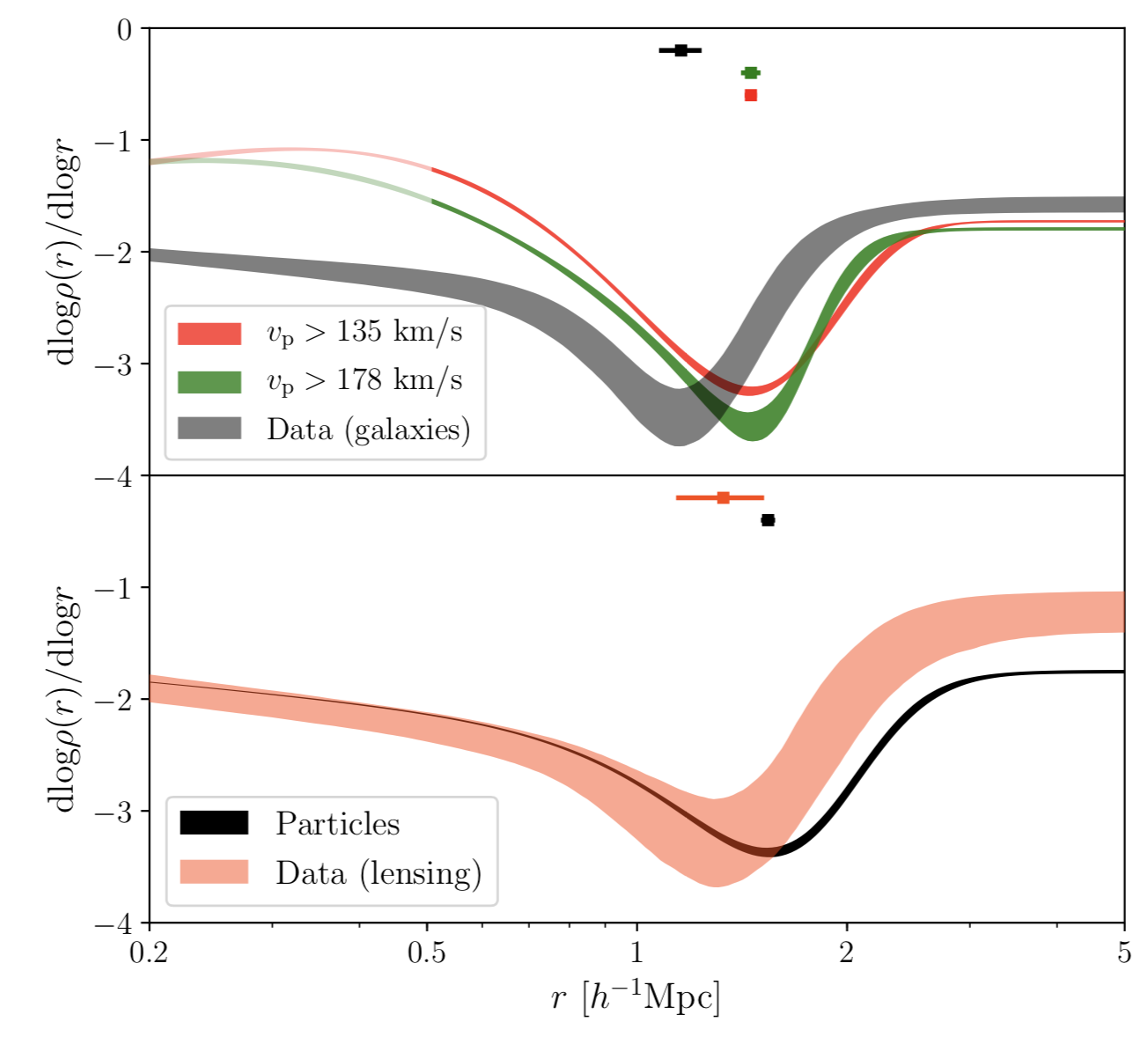
Halos are not generally spherical, however, and accretion is not actually smooth; i.e., halos accrete all kinds of substructure, with associated variation in particle density. In this more realistic scenario the caustic is not as sharp as the idealized case and is washed out in the density profile. However, recently it was found (by Diemer & Kravtsov, 2014 -- and note that all references are linked to the source papers at the end of this article), that the slope of the density profile, which is a measure of how quickly the density changes with distance from the center of the halo, can differ significantly in the outer profiles of halos from the standard profile which cosmologists know dark matter follows. In fact, in regions near the virial radius the slope can become extremely steep for certain populations of halos that are growing very fast.
Diemer & Kravtsov also found that the location of the minimum of the slope in the density profile is primarily a strong function of how fast the halo is growing in mass (its mass accretion rate). In Figure 3 below we see that the logarithmic slope of the halo in the outskirts goes to the value of about -4, beyond which it slowly climbs back up, steadily approaching the background value of zero. This steepening of slope in fact corresponds to the boundary of the halo. The minimum of the slope corresponds to the radius that separates the multi-streaming or virialized region from the infall region of the halo, as was shown when compared to the phase space diagrams in Adhikari, et al., 2014.
The boundary of the halo depends intimately on its growth history. This boundary moves with accretion rate and the density relative to the background at which this boundary exists depends on the redshift at which the halo forms. In Adhikari et al., 2014, we found a simple model to understand the location of this boundary by solving the equation of motion of the shell in a halo that is growing with time in an expanding Universe. We constructed a toy model that follows its motion in a standard dark matter (Navarro-Frenk-White) potential. We found that this model can accurately predict the location of this feature for a large range of accretion rates and redshifts that are typical in dark matter-only simulations, despite the fact that halos come in many different shapes, sizes, and histories.
In fact, we found that predictions from our simple spherical accretion model with basically no free parameters match dark matter-only simulations well, even when many halos are stacked together. This implies that the underlying physics that sets the location of this feature is universal and easy to understand. The splashback radius then is essentially a dynamical signature of the halo that is visible in the slope of its density profile. The physics setting the behavior of this feature is straightforward, as it is essentially energy conservation in a gravitational field.
Splashback for subhalos
Dark matter halos grow hierarchically; particles first form smaller halos that fall into and live in larger ones, with the smaller halos being known as subhalos and the larger as hosts. Just like the splashback radius is expected to appear in the density profile of dark matter particles, it should also be present in the distribution of subhalos in their hosts, as they essentially follow the same gravitational dynamics as individual dark matter particles. Fortunately, galaxies reside in many of these subhalos that form before their entry into a larger host, making them the visible component of large halos that appear to be conglomerations of many such galaxies. These galaxy-subhalo objects fall into the host halo with the same velocities as dark matter particles and therefore have orbits like the particles themselves. Therefore, the splashback radius should be present in the slope of the density distribution of subhalos or galaxies.
However, the only difference between subhalos and dark matter particles is that subhalos with masses greater than about 1% of the host radius are subject to dynamical friction, which is a drag force that they experience when moving through an ambient medium of lower-mass particles. The momentum lost to the ambient medium leads to a net orbital energy loss and causes the apocenters (farthest points in orbit) of subhalo orbits to shrink in comparison to the dark matter particles. Low-mass subhalos do not feel significant effects of friction over their orbital times, and therefore have a splashback feature near that of the dark matter particles, while higher-mass ones have a smaller radius of turnaround.
While a lot of indirect evidence for dynamical friction exists in the Universe, the movement of the splashback radius with subhalo mass is a direct detection of this effect. In observations, galaxy magnitude is correlated with subhalo mass—in other words, brighter galaxies live in more massive halos—and in Adhikari et al., 2016, we measured the movement of splashback radius with galaxy magnitude in low-mass cluster halos.
However, the first measurement of the splashback radius was made in the distribution of galaxies around massive cluster halos in More, et al., 2015. The slope of the density profile of galaxies was measured using galaxies from the SDSS surveys around clusters identified optically with the RedMaPPer algorithm. The slope of the number density profile of the galaxies (i.e., how many galaxies there are per unit volume in these galaxy clusters) showed a sharp drop in a narrow localized region (shown for DES data, which exhibited analogous behavior, in Fig. 3) . Surprisingly, however, when compared with theoretical expectations from simulations this feature appeared at a smaller cluster-centric radius.
As the physics that sets the scale of this feature is simple and its existence is almost inevitable in an LCDM universe, this discrepancy is somewhat puzzling. This discovery was also confirmed in Baxter, et al., 2016, and Chang, et al., 2017, using DES data, which covers a wider field than the SDSS (again, Fig. 3). Furthermore, Chang, et al., measured the feature in weak lensing profiles of galaxies around the clusters as well. Weak lensing (previously discussed in this August 2017 KIPAC blogpost) is the mild distortion of galaxy shapes in the background of massive objects that bend the path of light emanating from these galaxies, making them appear distorted. Measuring these distortions can give us an estimate of the amount of matter and its distribution in the massive foreground object that lenses the light. Consistent with previous work, Chang, et al., 2017, found that the location of the splashback radius measured from weak lensing is also at a smaller radius than expected from CDM simulations. This may possibly indicate some new physics, which we will revisit below, or systematics related to the cluster identification. To address the second concern, more recently Hyeon-Shin, et al. measured this feature around clusters identified in a completely independent way using SPT and ACT surveys and found that the location of the feature is more consistent with theoretical expectations (see Fig. 4). However, given the low signal to noise of the measurement, it is not yet possible to rule out the the discrepancy definitively.
Hints of new physics?
As mentioned earlier, the physics of the splashback radius is fairly straightforward: it’s simply the gravitational evolution of a shell in an expanding Universe, in a time-changing potential and following simple arguments of energy conservation. We might therefore expect that scenarios that affect the nature of gravity and background expansion may imprint their signatures on this feature. We investigate the effect of modified gravity and different models of dark energy on the location of the splashback radius in Adhikari, et al., 2018.
We find that certain models of modified gravity (such as the complex modifications of General Relativity that go by the names of the f(R) and nDGP extensions) may give rise to significant differences in the location of this feature in subhalos as well as particles. The basic idea is that in models of gravity that enhance gravitational effects, the increased forces cause objects to fall faster and with higher kinetic energy, leading to a larger radius for the second turnaround or splashback. In additions, due to increased velocities at infall, the force of dynamical friction becomes weaker when compared to gravity, leading to massive subhalos turning around closer where dark matter particles turn around than expected in LCDM.
Apart from modified gravity and dark energy, I am also currently investigating the effect of the inherent nature of dark matter on splashback, namely, how self-interactions in dark matter could result in a change in splashback location.
Insights from the far edge
Finally, another application of the physics of splashback that is interesting to me is to connect it with the understanding of galaxy evolution. Namely, the splashback is basically a scale in the dark matter halo that represents the location of second turnaround, or its first orbital apocenter. If the distribution of a population of galaxies around halos shows a splashback feature it is likely that the members of that sample have completed at least one pericentric passage and have reached turnaround. While it is known that galaxies turn red and dead in cluster environments, how rapidly blue disk-like galaxies cease to form stars and turn into red, elliptical galaxies is a standing question in galaxy formation and evolution. If the splashback radius can be used as a clock and measured in galaxies of different colors, we may be able to distinguish between different models of `quenching’, or the suppression of star formation in galaxies in clusters.
It turns out that simply properly defining and finding the edge of galaxy clusters can be a fertile arena for investigating not only our current scenarios of galaxy and star formation, but possibly for giving us hints into which directions we will need to go to probe extensions to Einstein’s long-standing and very robust theory of gravity!
Related reading and cited papers
- The Splashback Feature around DES Galaxy Clusters: Galaxy Density and Weak Lensing Profiles
- Measurement of the Splashback Feature around SZ-selected Galaxy Clusters with DES, SPT and ACT
